ملاحظات دراسة التعلم الآلي (ثلاثة عشر) Random Forest (RandomForest)
غابة عشوائية (RandomForest)
1. إعداد المعرفة
1.1 شجرة القرار
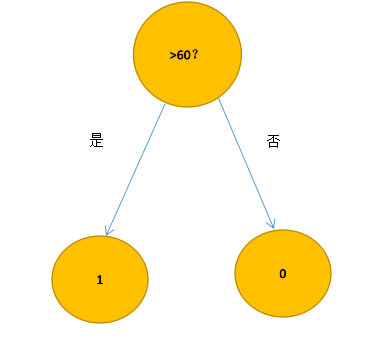
تُعد شجرة القرار هي أبسط نموذج للتعلم الآلي ، وبدون النظر في المواقف المعقدة الأخرى ، يمكننا وصف شجرة القرارات في جملة واحدة: إذا كانت النتيجة 60 أو أكثر ، فحينئذٍ تمر. (إذا-ثم البيان)
هذا هو أبسط نموذج لشجرة القرار ، حيث نقوم بتسمية التمرير والفشل على التوالي ، باستخدام التمريرة (1) والفشل (0) ، ثم تبدو شجرة القرارات كما يلي:
لكننا بالكاد ندع أجهزة الكمبيوتر تقوم بهذه المهمة البسيطة ، فنجعل الموقف أكثر تعقيدًا
أذكر مثال لمقال آخر
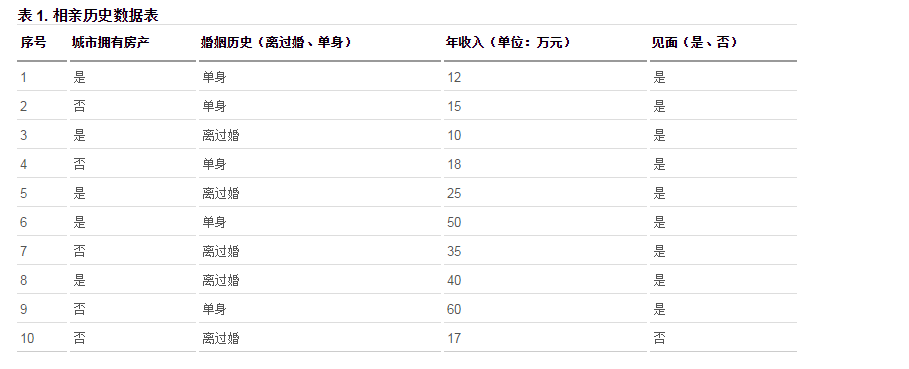
هذا جدول إحصائي حول ما إذا كانت الفتيات يختارن مقابلة الرجال ذوي الظروف المختلفة ، وما إذا كان الاجتماع في الصورة هو النتيجة التي نحتاج إلى تصنيفها ، لذلك في النهاية ، نتائجنا ليست أكثر من نعم ولا. هذه مشكلة في التصنيف الثنائي ، ولكن هناك الكثير من الشروط التي يجب الحكم عليها ، والآن ليس مجرد حكم للحصول على نتائج ، ولكن من الصورة أعلاه نجد سجلاً بنتيجة سلبية ، لذلك إذا كان هناك رجل في المدينة بدون خاصية ، دخل سنوي أقل من 17 واط ، والطلاق ، يمكنك التنبؤ بأن الفتاة لن تقابله.
ثم السؤال الذي يطرح نفسه ، كيف يمكن بناء شجرة قرار في مثل هذا الموقف المعقد؟
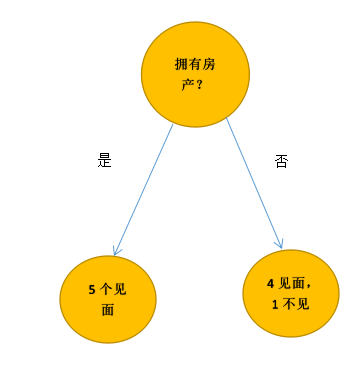
وفقًا لخصائص ما إذا كانت المدينة تمتلك عقارات ، يتم تقسيم الأشخاص العشرة إلى فئتين.
نتيجة التصنيف هذه ليست جيدة جدًا ، لأنها لا تفصل الاجتماع والاجتماع تمامًا ، وفي الخوارزمية بالطبع ، لا يمكننا تقييم نتيجة التصنيف بناءً على "إحساسنا".نحن بحاجة إلى استخدام رقم لتمثيله.
1.2 جيني النجاسة
انتروبيا المعلومات
هذه هي نظرية المعلوماتكمية المعلوماتوانتروبيا المعلوماتالمعرفة。
كمية المعلومات: كمية المعلومات هي مقياس للمعلومات ، تمامًا كما يتم قياس درجة الحرارة بالدرجات المئوية. يرتبط حجم المعلومات باحتمال وقوع الحدث.
على سبيل المثال: في فصل الشتاء في هاربين ، ذكرت رسالة أن درجة الحرارة في هاربين ستكون 30 درجة مئوية غدًا ، وسيؤدي هذا الحدث بالتأكيد إلى إحساس لأنه لديه احتمال ضعيف (كمية كبيرة من المعلومات). اليوم هو الصيف ، وقد لا تعتبر "درجة حرارة الغد 30 درجة مئوية" خبراً ، لأن درجة حرارة الصيف البالغة 30 درجة مئوية طبيعية للغاية والاحتمال كبير جدًا (نقطة المعلومات صغيرة جدًا)
يمكن أن نلاحظ من هذا المثال أن كمية المعلومات الخاصة بحدث عشوائي مرتبطة عكسيا باحتمال حدوثه.
محتوى المعلومات لحدث معرف بواسطة Shannon هو: I (X) = log2 (1 / p) حيث p هو احتمال حدوث الحدث X
انتروبيا المعلومات:Entropy يمكن للمتغير العشوائي X أن يمثل الأحداث العشوائية ، ويصبح الحرف العشوائي المقابل X = xi ، ثم تعريف entropy هو مقدار المعلومات الموزون لـ X.
H(x) = p(x1)I(x1)+...+p(xn)I(x1)
= p(x1)log2(1/p(x1)) +.....+p(xn)log2(1/p(xn))
= -p(x1)log2(p(x1)) - ........-p(xn)log2(p(xn))
حيث يمثل p (xi) احتمال حدوث xi
على سبيل المثال ، هناك 32 فريق كرة قدم يلعبون ، يتمتع كل فريق بنفس القوة ، وبالتالي فإن احتمال فوز كل زوج هو 1/32.
ثم من الصعب للغاية تخمين فريق كرة القدم الذي يفوز ، كما يمكن استخدام إنتروبيا H (x) = 32 * (1/32) log (1 / (1/32)) = 5 في هذا الوقت كمعيار لدرجة الإرباك .
تخيل لو كان أحد الفرق الـ 32 هو ميلان ، والآخر 31 زوجًا هم فريق Beiyou Computer 1st ، من الدرجة الثانية ، ... من المرتبة 31 ، إذن هناك احتمال واحد فقط بأن يكون فوز ميلان 100٪ ، والآخرون 0 ٪ ، انتروبيا هذا النظام
هذا هو 1 * سجل (1/1) = 0.هذا النظام مطلوب بالفعل ، والنتروب صغير جدًا ، في حين أن النظام السابق الذي يحتوي على إنتروب 5 هو خارج الترتيب.
جيني النجاسة
المعنى العام لـ Gini Impurity هو احتمال أن يصبح الحدث العشوائي نقيضه.
على سبيل المثال ، حدث عشوائي X ، P (X = 0) = 0.5 ، P (X = 1) = 0.5
نقاء Gini هو P (X = 0) * (1-P (X = 0)) + P (X = 1) * (1-P (X = 1)) = 0.5
حدث عشوائي Y ، P (Y = 0) = 0.1 ، P (Y = 1) = 0.9
نقاء Gini هو P (Y = 0) * (1-P (Y = 0)) + P (Y = 1) * (1-P (Y = 1)) = 0.18
من الواضح أن X أكثر إرباكًا من Y ، لأن كلاهما 0.5 ويصعب تحديد أيهما حدث. Y أكثر تحديدًا ، واحتمال حدوث Y = 0 مرتفع جدًا. أصغر النجاسة جيني ، أصغر النقاء.
يمكن أيضًا استخدام نقاء Gini كمقياس لدرجة تشويش النظام.
نقاء جيني هو مقياس لمدى جودة التصنيف
قيمته هي: 1- مجموع مربعات نسبة كل تسمية إلى المجموع. هذا هو 1-=mi = 1fi2
بالنسبة للنتائج المذكورة أعلاه ، يتم تقسيم المجموعة الإجمالية D إلى مجموعتين D1 ، D2 ، على افتراض أن الاجتماع هو 1 ، والاجتماع هو 0.
إذاً فإن شوائب D1 هي 1-f1 ^ 2-f0 ^ 2 ، والرقم الإجمالي هو 5 ، والاجتماع يجتمع جميعًا ، ثم f1 = 1 ، f0 = 0 ، والنتيجة هي 0
شوائب D2 هي 1-f1 ^ 2-f0 ^ 2 ، f1 = 0.8 ، f0 = 0.2 ، والنتيجة 0.32
حسنًا ، إذن فإن شوائب Gini الخاصة بنتيجة التصنيف بأكملها هي منتج D1 / D و 0 بالإضافة إلى منتج D2 / D و 0.32 ، وهو 0.16
تمثل قيمة Gini "درجة نقاء" نتيجة تصنيف معينة ، ونأمل أن تكون درجة نقاء النتيجة عالية جدًا ، لذلك ليست هناك حاجة لمعالجة هذه النتيجة.
يمكن أن يتبين من التحليل أعلاه أنه كلما كانت قيمة Gini أصغر ، كلما زادت درجة نقاءها وكانت النتيجة أفضل.
ثالثا ، جيل الأشجار القرار
في المثال الأول ، "إذا كانت النتيجة 60 أو أكثر ، ثم تجتاز" ، فإن خطوة إنشاء شجرة قرار هي أولاً تحديد الميزة ، "النتيجة" ، ثم تحديد القيمة الحرجة ، "> = 60"
1. ينطبق الأمر نفسه على الحالات المعقدة ، فبالنسبة لكل ميزة ، ابحث عن نقطة تجزئة تقلل من قيمة Gini (يمكن أن تكون نقطة التقسيم هذه بمثابة حكم مثل> أو <أو> = أو = أو! =) ، ثم قارن يتم استخدام أصغر قيمة Gini بين كل ميزة كنقطة تجزئة الأمثل للميزة المثلى الحالية (ويشمل ذلك في الواقع خطوتين ، اختيار الميزة المثلى واختيار نقطة التقسيم الأمثل).
2. بعد اكتمال الخطوة الأولى ، سيتم إنشاء عقدتين للورقة ، ونحكم على العقدتين الورقتين ونحسب ما إذا كانت قيمة Gini الخاصة بها صغيرة بدرجة كافية (إذا كان الأمر كذلك ، لم تعد تصنف كأوراق)
3. باستخدام العقد الورقية التي تم الحصول عليها في الخطوة السابقة كمجموعة جديدة ، قم بإجراء تصنيف الخطوة 1 لتوسيع عقدتي أوراق جديدتين (بالطبع ، تصبح هذه العقدة هي العقدة الأصل)
4. تتكرر الحلقة حتى لا توجد أي عقد أوراق لا تفي بقيمة Gini
الرابعة ، وأوجه القصور في الأشجار القرار
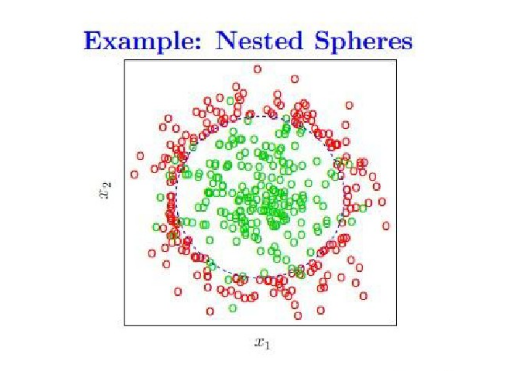
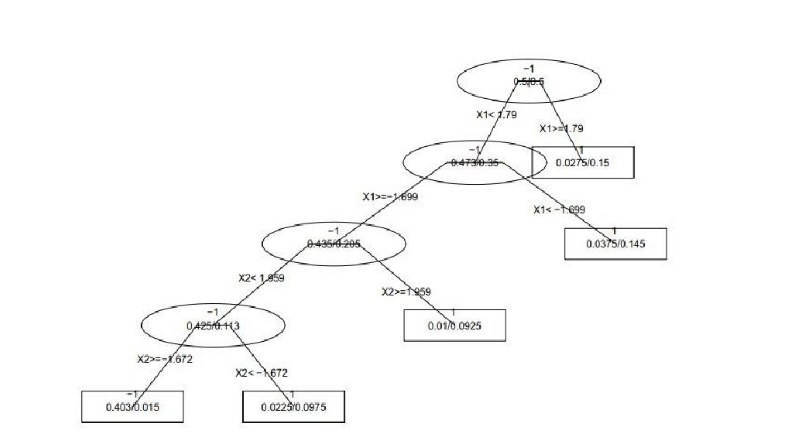
نحن نستخدم شجرة اتخاذ القرار لتقسيم العديد من النقاط على المستوى إلى فئتين ، ولكل نقطة (x1 ، x2) ميزتين ، يتم عرض عملية التصنيف أدناه.
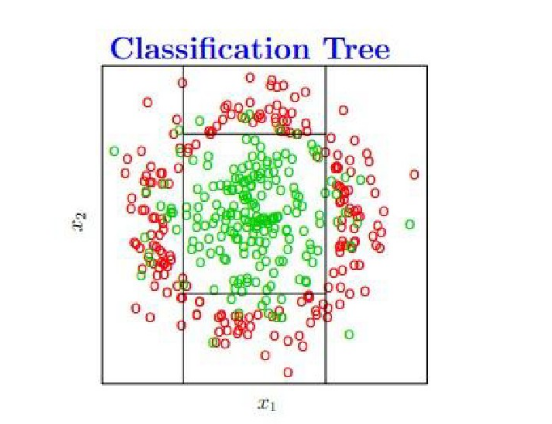
تحتوي شجرة القرارات النهائية على أربع نقاط تجزئة ، ويتم عرضها على الرسم البياني على النحو التالي ، وطالما تقع في المنطقة المستطيلة المركزية ، يكون اللون الافتراضي أخضر ، وإلا يكون أحمر.
ومع ذلك ، فإن هذه الحالة هي حالة يكون فيها اختيار معلمة التصنيف معقولًا (لا تمانع في أن بعض النقاط الخضراء تقع على الهامش) ، لكن عندما نتدرب ، نحتاج إلى تصنيف جميع النقاط الخضراء دون أخطاء (أي أن اختيار المعلمة ليس غاية (الموقف المعقول) ، ستنتج شجرة القرارات ملاءمة أكثر مما يؤدي إلى ضعف القدرة على التعميم.
خمسة ، غابة عشوائية
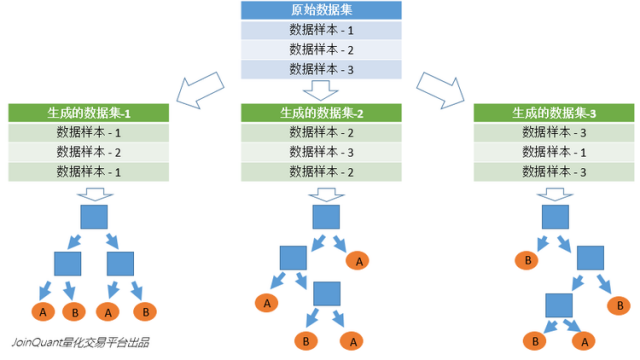
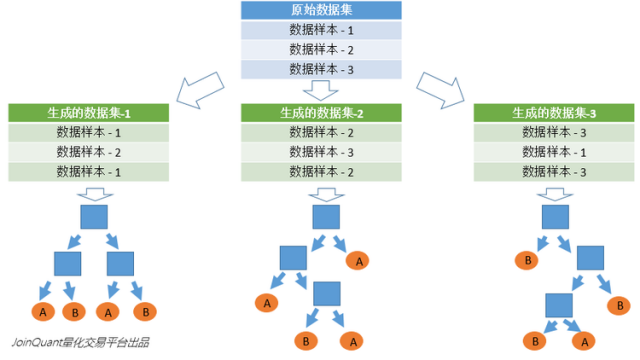
بالنظر إلى أوجه القصور في الأشجار القرار التي هي عرضة لل overfitting ،تستخدم الغابة العشوائية آلية تصويت لأشجار قرارات متعددة لتحسين أشجار القرارنحن نفترض أن الغابة العشوائية تستخدم أشجار القرار m ، ثم نحتاج إلى إنشاء عدد معين من مجموعات العينات لتدريب كل شجرة.إذا كان من الواضح أنه من غير المرغوب فيه تدريب أشجار قرار m مع عينات كاملة ، يتم تجاهل تدريب العينة الكامل قانون العينات المحلية ضار بقدرة تعميم النموذج
تستخدم طريقة إنشاء عينات n طريقة Bootstraping ، وهي طريقة أخذ عينات مع الاستبدال ، والتي تولد عينات n.
يتم الحصول على النتيجة النهائية باستخدام استراتيجية Bagging ، أي آلية التصويت بالأغلبية
طريقة توليد الغابات العشوائية:
1. توليد عينات ن من خلال إعادة أخذ العينات من مجموعة العينة
2. على افتراض أن عدد ميزات العينة هو ، حدد k ميزات في n للعينات واحصل على أفضل نقطة تجزئة عن طريق إنشاء شجرة قرار.
3. كرر مرات m لإنشاء الأشجار قرار م
4. آلية التصويت بالأغلبية لعمل تنبؤات
(تجدر الإشارة إلى أن m هو عدد الدورات ، n هو عدد العينات ، وتشكل العينات مجموعة عينات التدريب ، ويتم إنشاء مجموعات العينات هذه في دورات m)
ستة ، ومكافحة الغابات العشوائية
مجموعة البيانات:
مجموعة بياناتنا مأخوذة من موقع ويب معروف لمسابقة التنقيب عن البيانات ، وهي عبارة عن استطلاع حول بقاء السياح على متن السفينة Titanic. يمكنك تنزيله من هنا:https://www.kaggle.com/c/titanic/data
قراءة البيانات
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
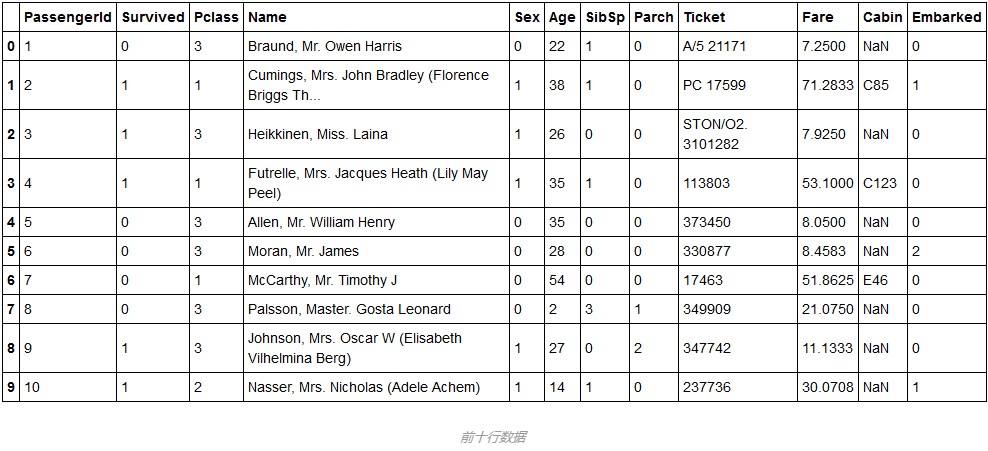
train = pd.read_csv("E:/train.csv", dtype={"Age": np.float64},)
train.head(10)بعد قليل من التحليل ، يمكننا تصفية المتغيرات المتعلقة ببقاء السائح: Pclass ، أو الجنس ، أو العمر ، أو SibSp ، أو Parch ، أو Fare ، أو Embarked ، وبصفة عامة ، اسم السائح ، وعدد التذكرة التي اشتراها ، يجب أن يكون ظروف البقاء على قيد الحياة تأثير يذكر.
len(train_data)
out:891
لدينا ما مجموعه 891 بيانات ، ما يقرب من 900 ، نستخدم 600 كبيانات تدريب ، والباقي 291 كبيانات اختبار. من خلال الضبط المستمر لمعلمات الغابة العشوائية ، اكتشف أدق مجموعة عشوائية للتنبؤ في نتائج الاختبار نموذج.
قبل التجربة المحددة ، دعونا نلقي نظرة على المتغيرات التي تحتاج إلى الاهتمام باستخدام نموذج الغابة العشوائي:
في sklearn ، نموذج وظيفة الغابة العشوائية هو:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
oob_score=False, random_state=None, verbose=0,
warm_start=False)
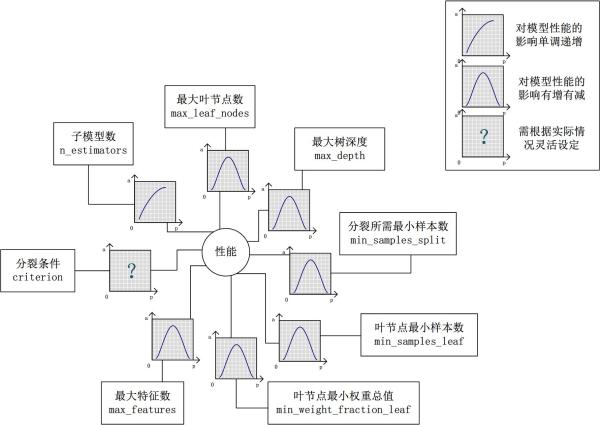
تحليل المعلمة
A. max_features:
تتيح مجموعة التفرعات العشوائية الحد الأقصى لعدد الميزات لشجرة قرار واحدة. يوفر Python خيارات متعددة لأكبر عدد من الميزات. هؤلاء قليل منهم:
Auto / None: ببساطة حدد كل الميزات ويمكن لكل شجرة استخدامها. في هذه الحالة ، لا توجد قيود على كل شجرة.
sqrt: يتيح هذا الخيار لكل شجرة فرعية الاستفادة من الجذر التربيعي لإجمالي عدد الميزات. على سبيل المثال ، إذا كان العدد الإجمالي للمتغيرات (الميزات) هو 100 ، فيمكن أن تستغرق كل شجرة فرعية 10 منها فقط. "Log2" هو نوع آخر مماثل من الخيار.
0.2: يسمح هذا الخيار لكل شجرة فرعية من مجموعة تفرعات عشوائية باستخدام 20٪ من عدد المتغيرات (الميزات). إذا كنا نريد دراسة دور الميزة x٪ ، فيمكننا استخدام التنسيق "0.X".
كيف تؤثر المزايا القصوى على الأداء والسرعة؟
يمكن أن تؤدي زيادة الحد الأقصى للخصائص بشكل عام إلى تحسين أداء النموذج ، لأنه في كل عقدة ، لدينا المزيد من الخيارات للنظر فيها. ومع ذلك ، هذا ليس صحيحًا بالضرورة ، لأنه يقلل من تنوع شجرة واحدة ، والتي تعد ميزة فريدة للغابات العشوائية. ومع ذلك ، يمكنك التأكد من تقليل سرعة الخوارزمية عن طريق زيادة الحد الأقصى للميزات. لذلك ، تحتاج إلى التوازن بشكل صحيح واختيار أفضل الميزات.
B. n_estimators:
عدد الأشجار الفرعية التي تريد إنشاؤها قبل استخدام الحد الأقصى لعدد الأصوات أو المتوسط للتنبؤ. يمكن أن توفر المزيد من الأشجار الفرعية أداءً أفضل للطراز الخاص بك ، ولكن في نفس الوقت ، اجعل الشفرة أبطأ. يجب عليك اختيار قيمة عالية قدر الإمكان ، طالما أن المعالج قادر على تحملها ، لأن هذا يجعل تنبؤاتك أفضل وأكثر استقرارًا.
C. min_sample_leaf:
إذا كنت قد كتبت شجرة قرار من قبل ، فيمكنك تقدير أهمية أصغر حجم ورقة للنموذج. الورقة هي عقدة نهاية شجرة القرار. تُسهل الأوراق الأصغر على النموذج التقاط الضوضاء في بيانات التدريب. بشكل عام ، أفضل تعيين الحد الأدنى لعدد العقد الورقية على أكثر من 50. في حالتك الخاصة ، يجب أن تجرب أكبر عدد ممكن من أنواع أوراق الشجر لإيجاد النوع الأمثل.
فيما يلي نقوم بضبط المعلمات الثلاث المذكورة أعلاه: أولاً ، المعلمة A. نظرًا لوجود سبعة أو ثمانية مقاطع بيانات فقط في بياناتنا ، فإننا ببساطة نختار جميع الميزات ، لذلك نحن بحاجة فقط إلى يتم ضبط اثنين من المتغيرات المتبقية.
في خوارزمية الغابة العشوائية التي تأتي مع sklearn ، يجب أن تكون قيمة الإدخال عددًا صحيحًا أو رقمًا عائمًا ، لذلك نحتاج إلى معالجة البيانات مسبقًا وتحويل السلسلة إلى رقم صحيح أو رقم النقطة العائمة:
def harmonize_data(titanic):
# ملء البيانات الفارغة وتحويل بيانات السلسلة إلى تمثيل صحيح
# بالنسبة للحقل العمري المفقود ، فإننا نستبدل بمتوسط جميع الأعمار
titanic["Age"] = titanic["Age"].fillna(titanic["Age"].median())
# الجنس ذكر: استبدال بـ 0
titanic.loc[titanic["Sex"] == "male", "Sex"] = 0
# الجنس أنثى: استبدال 1
titanic.loc[titanic["Sex"] == "female", "Sex"] = 1
titanic["Embarked"] = titanic["Embarked"].fillna("S")
titanic.loc[titanic["Embarked"] == "S", "Embarked"] = 0
titanic.loc[titanic["Embarked"] == "C", "Embarked"] = 1
titanic.loc[titanic["Embarked"] == "Q", "Embarked"] = 2
titanic["Fare"] = titanic["Fare"].fillna(titanic["Fare"].median())
return titanic
train_data = harmonize_data(train)الرمز أعلاه ينظف البيانات الأصلية ، ويملأ البيانات المفقودة ، ويحول بيانات السلسلة إلى بيانات int.
في العمل التالي ، نبدأ في تقسيم بيانات التدريب وبيانات الاختبار. إجمالي البيانات هو 891. نستخدم 600 مجموعة بيانات تدريب ، ويتم استخدام الـ 291 المتبقية كمجموعات بيانات اختبار.
# قائمة الحقول التي لها تأثير على نتائج البقاء على قيد الحياة
predictors = ["Pclass", "Sex", "Age", "SibSp", "Parch", "Fare", "Embarked"]
# تخزين قيم المعلمات المختلفة والدقة المقابلة ، كل عنصر هو الثلاثي (أ ، ب ، ج)
results = []
# قيمة المعلمة أصغر عقدة ورقة
sample_leaf_options = list(range(1, 500, 3))
# عدد المعلمات شجرة القرار
n_estimators_options = list(range(1, 1000, 5))
groud_truth = train_data['Survived'][601:]
for leaf_size in sample_leaf_options:
for n_estimators_size in n_estimators_options:
alg = RandomForestClassifier(min_samples_leaf=leaf_size, n_estimators=n_estimators_size, random_state=50)
alg.fit(train_data[predictors][:600], train_data['Survived'][:600])
predict = alg.predict(train_data[predictors][601:])
# استخدم الثلاثي لتسجيل min_samples_leaf الحالي ، n_estimators ، والدقة في مجموعة بيانات الاختبار
results.append((leaf_size, n_estimators_size, (groud_truth == predict).mean()))
# مقارنة النتائج الحقيقية مع النتائج المتوقعة لحساب الدقة
print((groud_truth == predict).mean())
# طباعة ثلاثية بأعلى دقة
print(max(results, key=lambda x: x[2]))بشكل عام ، لا تتسبب معلمات الضبط في تقلبات كبيرة للغابات العشوائية ، فبخلاف الشبكات العصبية ، يمكن للغابات العشوائية أن تحقق نتائج جيدة حتى مع المعلمات الافتراضية. في مثالنا ، من خلال توليف تقريبي ، يمكننا تحقيق دقة تنبؤ تبلغ 84٪ في مجموعة الاختبار.
أرفق كل الكود: (مدة التشغيل أطول)
__author__ = 'Administrator'
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
train = pd.read_csv("E:/train.csv", dtype={"Age": np.float64},)
def harmonize_data(titanic):
# ملء البيانات الفارغة وتحويل بيانات السلسلة إلى تمثيل صحيح
titanic["Age"] = titanic["Age"].fillna(titanic["Age"].median())
titanic.loc[titanic["Sex"] == "male", "Sex"] = 0
titanic.loc[titanic["Sex"] == "female", "Sex"] = 1
titanic["Embarked"] = titanic["Embarked"].fillna("S")
titanic.loc[titanic["Embarked"] == "S", "Embarked"] = 0
titanic.loc[titanic["Embarked"] == "C", "Embarked"] = 1
titanic.loc[titanic["Embarked"] == "Q", "Embarked"] = 2
titanic["Fare"] = titanic["Fare"].fillna(titanic["Fare"].median())
return titanic
train_data = harmonize_data(train)
predictors = ["Pclass", "Sex", "Age", "SibSp", "Parch", "Fare", "Embarked"]
results = []
sample_leaf_options = list(range(1, 500, 3))
n_estimators_options = list(range(1, 1000, 5))
groud_truth = train_data['Survived'][601:]
for leaf_size in sample_leaf_options:
for n_estimators_size in n_estimators_options:
alg = RandomForestClassifier(min_samples_leaf=leaf_size, n_estimators=n_estimators_size, random_state=50)
alg.fit(train_data[predictors][:600], train_data['Survived'][:600])
predict = alg.predict(train_data[predictors][601:])
# استخدم الثلاثي لتسجيل min_samples_leaf الحالي ، n_estimators ، والدقة في مجموعة بيانات الاختبار
results.append((leaf_size, n_estimators_size, (groud_truth == predict).mean()))
# مقارنة النتائج الحقيقية مع النتائج المتوقعة لحساب الدقة
print((groud_truth == predict).mean())
# طباعة ثلاثية بأعلى دقة
print(max(results, key=lambda x: x[2]))ملخص نماذج الغابات العشوائية
تعد الغابة العشوائية نموذجًا رائعًا ، فمن وجهة نظر استخدام مشروعي ، تتمتع بالكفاءة العالية لتصنيف مجموعات بيانات الميزات متعددة الأبعاد ، ويمكنها أيضًا اختيار أهمية الميزات. كفاءة التشغيل و دقته عالية ، و سهل التنفيذ نسبيا. ومع ذلك ، في حالة وجود ضوضاء كبيرة نسبياً في البيانات ، سيحدث التجهيز الزائد ، ولا تزال مساوئ التداخل الزائد أكثر فتكًا بالغابات العشوائية.
رابط المرجع
[1]https://blog.csdn.net/mao_xiao_feng/article/details/52728164
توصية ذكية
Random Forest RandomForestClassifier لتعلم الآلة
Random Forest RandomForestClassifier لتعلم الآلة كما هو موضح:...
RandomForest / Adaboost لسلسلة التعلم الآلي
جدول المحتويات RandomForest قواعد لتوليد كل شجرة: تحتوي الغابة العشوائية على نوعين من العشوائيات: Adaboost عملية التكرار: النتيجة المرجحة: انظر URL: RandomForest Random Forest هي خوارزمية تدمج العديد ...
Random Forest
غابة عشوائية - غابة عشوائية تحدثت المقالة السابقة عن أشجار القرار ، في هذه المقالة سنتحدث عن مجموعة من الأشجار ، غابة عشوائية. ①Aggregation Model لا تزال الغابة العشوائية لم تفلت من نموذج التجميع ، فق...
Random Forest
...
Random Forest
أخذ العينات الذاتية بالنظر إلى مجموعة البيانات D التي تحتوي على عينات m ، قمنا بتجميعها لإنشاء مجموعة بيانات D ': اختر عينة عشوائيًا من D في كل مرة وضع نسخة منها في D ' ثم أعد العينة إلى مجموعة البيان...
ربما يعجبك أيضا
Random Forest
الغابات العشوائية هي خوارزمية متكاملة تتكون من شجرة القرار. يمكن أن يكون لديه أداء جيد في كثير من الحالات. ستقدم هذه المقالة المفاهيم الأساسية للغابات العشوائية، 4 خطوات البناء، وتقييم المقارنة...
Random Forest
دليل المقالات غابة عشوائية مبدأ اساسي اختيار البيانات العشوائية اختيار عشوائي لخصائص الاختيار sklearn.ensemble.randomforestClassifier المعلمة sklearn.ensemble.randomforestClassifier خصائص غابة عشوائية...
Random Forest
دليل المقالات غابة عشوائية مبدأ اساسي اختيار البيانات العشوائية اختيار عشوائي للميزات عشوائي forestclassifier المعلمة عشوائي forestclassifier سمة مصفوفة مشوشة عبر المصادقة بحث الشبكة أفضل معلمة عرض تو...
مكتبة تعلم الآلة بيثون - أساليب sklearn المتكاملة (التعبئة ، التعزيز ، Random Forest RF ، AdaBoost ، GBDT)
دليل تطوير مهندس المكدس الكامل (المؤلف: Luan Peng) Python سلسلة من البيانات التعليمية الهدف من طريقة التجميع هو الجمع بين نتائج التنبؤ لمقدرات أساسية متعددة تم إنشاؤها باستخدام خوارزمية تعلم معينة للح...
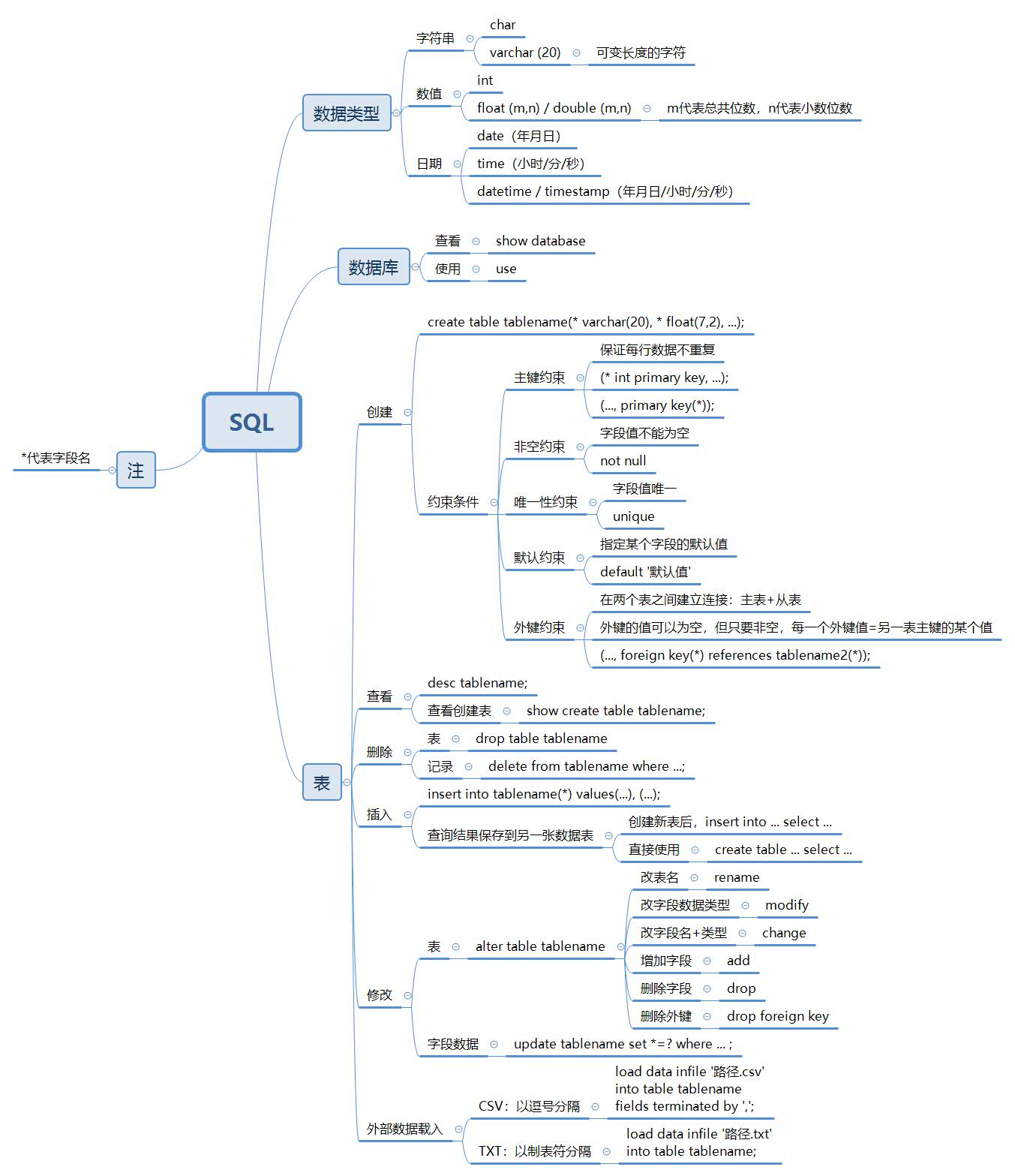
SQL 1
قاعدة البيانات 025-SQL 026-SQL 027-SQL 028-SQL 、 025-SQL – // :char(?),varchar(20) ,varchar // :int, float(m,n) / double(m,n) , m ,n // :date( ), time( / / ), datetime / timestamp( / / / ) &ndas...
المواد ذات الصلة
- [تعلم الآلة] Random Forest
- التعلم الآلي Sklearn-Random Forest
- التعلم المتكامل: Random Forest / GBDT / XGBoost (ملاحظات الدراسة 1)
- ملاحظات دراسة التعلم الآلي --- تنفذ Python غابة عشوائية RandomForest
- [التعلم الآلي] Random Forest رقم 4
- التعلم المتكامل Python Random Forest (مذكرات دراسة)
- جوليا تعلم الآلة في التعرف على صور الشخصيات باستخدام Random Forest
- [تعلُم الآلة] Random Forest ، Adaboost ، GBDT (مفصّل جدًا)
- محاضرة تقنيات التعلم الآلي لين Xuantian 10-Random Forest
- تنفيذ خوارزميات التعلم الآلي من الصفر (18) Random Forest
المواد شعبية
- مخطط الجدول الفرعي لقاعدة البيانات الفرعية Mysql
- [Li Jingshan PHP] Daily Larvel-20160907 | Respatcher-7
- MySQL: Problem: [Err] 1153 - Got a packet bigger than 'max_allowed_packet' bytes [Err] /*
- getFatt بواسطة ROS -تنفيذ البرمجة لمشترك المشترك
- 2019.07.30 [Learning STM32] فهم USB إلى PUT CINCULAL
- طريقتان للعثور على أطول سلسلة فرعية مشتركة
- تصميم نمط مصنع مجردة
- أسعد شجرة رقص DP
- بناء كتلة سولر-كلاود
- تم إغلاق اتصال مؤسسة Nuget VS2013: يحدث خطأ عند الإرسال
مقالة موصى بها
- ملخص لمولدات ومكررات بيثون
- اختبار خدمة الويب ساعي البريد
- Sqlalchemy ---------- مستوى لغة التعبير
- [أسئلة فرشاة إصبع السيف] تجد في الصفيفتين الأبعاد
- 2018-06-21 ضبط بايثون العمليات
- atext -question 2: العبارة تحتوي على عبارة أخرى تسبب القول الطويل أن القول الطويل غير فعال/يريد أن يكون عبارة بدلاً من شظية التعريف
- تستخدم BUSCO الملاحظات
- أداة تعميق القاتلة
- ملخص تعلم تخطيط ذاكرة اللغة C
- تثبيت بابل بوليفيل. دع أي دعم ES6